[통계기본] Sampling Distributions (표본 분포)와 Central Limit Theorem (중심극한정리)

---

1. 표본 분포

• 모집단(Population)으로 부터 많은 수의 표본집단(n)을 추출한다고 가정하여 나오는 표본샘플의 값들의 분포 추정값(Estimates)
• Hypothetical 이라는 점을 명심해야한다! 
• 정말 많은 수의 표본을 추출하게 되었을 때, 추정값은 정규분포(Normal Distribution) 처럼 보이게 된다. 이에 대한 정리가 중심극한정리

 

 

 

2. 중심극한 정리 (CLT, Central Limit Theorem)

• 모집단의 평균을 m, 표준편차를 σ라고 했을 때 모집단으로 부터 추출된 표본의 크기가 충분히 크다고 가정한다면 표본으로 부터 모집단의 평균을 추정할 수 있다는 명제의 기반이 되어주는 정리
  • https://drhongdatanote.tistory.com/57

[개념 통계] 중심극한 정리는 무엇이고 왜 중요한가?

• 모집단으로 부터 추출한 표준편차들의 추정값들의 분포는 정규분포 모양을 따르게 되는데, 표본의 크기가 클 수록 이 분포의 편차(Variance)는 계속해서 작아지게 된다. 즉, 분포의 범위(Range)가 작아진다는 뜻. 
• 이러한 분포의 편차를 다른 용어로 Sampling Error라고도 부르는데, 표본집단으로부터 모집단의 Value of Interests를 추정하고자 할 때 얼마나 정확하게 추정할 수 있는지에 대한 단서를 제공해주는 지표라고 할 수 있다.

시뮬레이션1. 샘플사이즈를 다르게하여 1,000개의 샘플을 추출하였을 경우

 

시뮬레이션2. 위와 같이 모든 경우에 대해 모집단의 co-efficients와 같은 평균값으로 수렴한다.

 

 

---

 

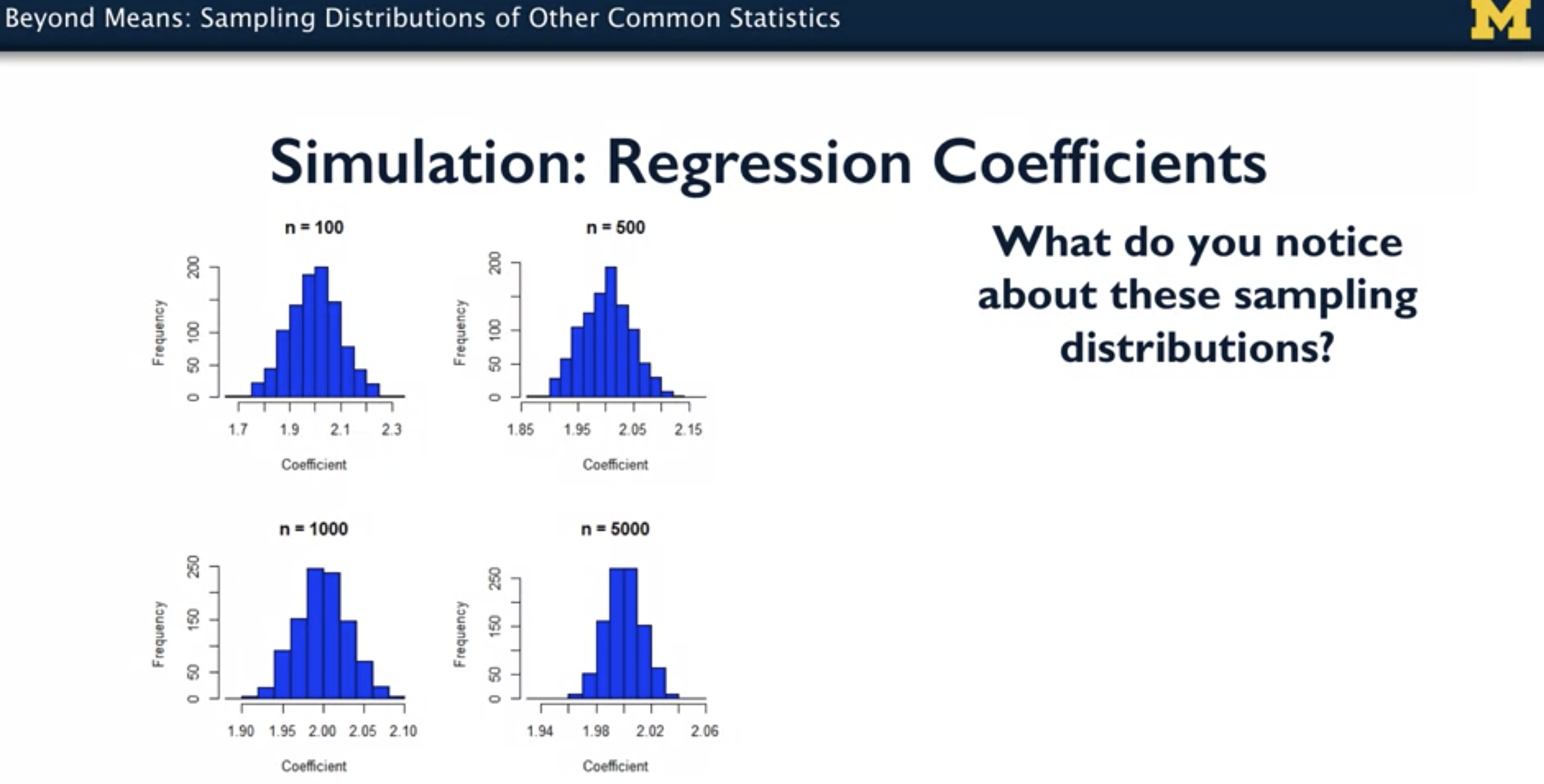
* Coursera의 Specialization 과정인 Statistics with Python 중 Understanding  and Visualizing Data with Python에 등장하는 내용입니다.

---

부족한 블로그에 방문해 주셔서 감사합니다.

잘못된 내용 수정 피드백은 댓글로 적어주세요.

감사합니다 :-)